
Distorsione del quadrilatero
La tabella 1 mostra le costanti reticolari degli strati magnetici CFMS per i cinque film studiati negli esperimenti. Le costanti del reticolo sono state misurate nelle direzioni parallele e perpendicolari al piano della pellicola. La differenza tra le due costanti rivela la presenza di deformazione quadrilatera nei campioni studiati.
sull’aereo (UNIn) e perpendicolare al piano (UNper ogniLe costanti di rete possono essere calcolate utilizzando le formule:
$$a_{in} = a_{0} + a_{0} \varepsilon_{11}$$
(1)
$$a_{per} = a_{0} + a_{0} \varepsilon_{33} ,$$
(2)
Dove UN0 è la costante reticolare dello strato magnetico rilassato (non vincolato) e H11 = H22 E H33 sono le deformazioni dello strato magnetico rispettivamente nel piano e perpendicolare al piano. inoltre
$$\varepsilon_{33} = – 2\frac{{c_{12} }}{{c_{11} }}\varepsilon_{11} ,$$
(3)
Dove C11 E C12Sono costanti elastiche. Risolvere equazioni. (1)-(3), abbiamo ottenuto i valori di pressione riportati nella Tabella 1. Lo abbiamo ipotizzato C11= 296GB C12= 172 GPa (dati interpolati per Co2Vesey & Company2 Composti MnSi presi dal rif.23). Dalla Tabella 1 si può vedere che l’applicazione di uno strato tampone aggiuntivo di Ag modifica la deformazione nel piano del film da trazione a compressione. Nel caso di campioni senza strato dielettrico Ag, diminuendo lo spessore dello strato magnetico da 50 a 15 nm aumenta la distorsione del quadrupolo di un ordine di grandezza. La costante reticolare per la struttura rilassata viene trovata per tutti i campioni UN0 = 5,659 ± 0,003Å.
Proprietà magnetoelastiche
La Figura 1 mostra le curve SMFMR con ampiezze normalizzate per i cinque campioni studiati nei nostri esperimenti.
Le curve SMFMR hanno un’ampiezza normale per i cinque campioni studiati nei nostri esperimenti. Un campo magnetico esterno è stato applicato lungo l’aereo [100] E [110] Asse cristallino del film epitassiale.
La Figura 1 mostra che cambiando lo spessore dello strato CFMS, così come applicando lo strato dielettrico Ag, cambia definitivamente l’anisotropia nel piano dei cristalli magnetici, che si manifesta cambiando i campi di risonanza misurati lungo [100] E [110] Assi. Studi più dettagliati sull’anisotropia dei cristalli magnetici sono presentati nella sezione successiva.
Per determinare le costanti magnetoelastiche degli strati magnetici indagati, abbiamo utilizzato la stessa procedura descritta in dettaglio nel nostro lavoro precedente21. Confrontando le ampiezze di due curve FMR, una delle quali è modificata dal campo magnetico (con ampiezza nota) e l’altra dalla deformazione, possiamo determinare lo spostamento della linea FMR causato dalla deformazione, come mostrato nella Tabella 2.
Le trasformazioni della linea FMR mostrate nella Tabella 2 sono state quindi utilizzate per calcolare le costanti magnetoelastiche. L’energia magnetica elastica può essere descritta dalla formula:
$$E_{me} = b_{1} \left( {\alpha_{1}^{2} \varepsilon_{11} + \alpha_{2}^{2} \varepsilon_{22} + \alpha_{3} ^ {2} \varepsilon_{33} } \right) + 2b_{2} \left( {\alpha_{1} \alpha_{2} \varepsilon_{12} + \alpha_{2} \alpha_{3} \varepsilon_ {23} + \alpha_{1} \alpha_{3} \varepsilon_{13} } \right){ },$$
(4)
Dove B1 E B2 Sono le costanti magnetiche elastiche cubiche. alfaIO è il coseno della direzione, e HIJ Sono le componenti del tensore di deformazione espresse nel sistema di coordinate associato al campione. Le costanti magnetoelastiche calcolate sono mostrate nella Tabella 3.
Simile ai campioni studiati nel rif.21proprietà magnetoelastiche anisotrope, cioè B1E B2 Le costanti per ciascun campione hanno grandezze diverse (per un campione isotropo, B1 = B2 ) e la sua dimensione B2 La costante è sempre superiore a B1 . Inoltre, le costanti magnetoelastiche cambiano anche con lo spessore dello strato magnetico e la loro grandezza può essere regolata applicando uno strato dielettrico aggiuntivo di Ag.
La magnetizzazione di saturazione degli strati magnetici misurata dal VSM era di 979 emu/cm3967 emu/cm3972 emu/cm3930 emu/cm3e 1040 emu/cm3 Rispettivamente per campioni da 15 nm, 30 nm, 50 nm, 30 nm/Ag e 50 nm/Ag. L’entità leggermente superiore della magnetizzazione di saturazione per il campione da 50 nm/Ag può indicare un miglioramento nell’ordinamento chimico per il campione più spesso con uno strato dielettrico aggiuntivo di Ag.
Anisotropia dei cristalli magnetici
Nel sistema di misurazione SMFMR non è possibile ruotare il campo magnetico esterno nel piano della pellicola. Per prendere ciascuna curva FMR mostrata nella Figura 1, il campione deve essere ricollegato. Pertanto, è molto difficile determinare in questo modo l’esatta dipendenza angolare del campo di risonanza. Inoltre, il campo magnetico esterno massimo ottenibile nel nostro sistema SMFMR era solo di circa 9500 Oe, rendendo impossibile l’identificazione del campo di risonanza perpendicolare al piano della pellicola e l’anisotropia dei cristalli magnetici ortogonali. Per questo motivo, sono stati eseguiti ulteriori esperimenti FMR utilizzando uno spettrometro Bruker EMX EPR.
La Figura 2 mostra le dipendenze angolari del campo di risonanza FMR nel piano per i tre campioni studiati nei nostri esperimenti. La simmetria quadrilatera delle curve conferma che l’anisotropia cubica magneto-cristallina è dominante nel piano del film. Si può anche vedere che aumentando lo spessore dello strato CFMS e aggiungendo lo strato dielettrico Ag si riduce questa anisotropia (cioè le curve diventano più circolari). Per i campioni senza lo strato tampone Ag, così come per il campione più sottile di 30 nm con tampone Ag, la quadruplice simmetria dominante è leggermente rotta indicando la presenza di una componente di simmetria uniassiale nel piano.
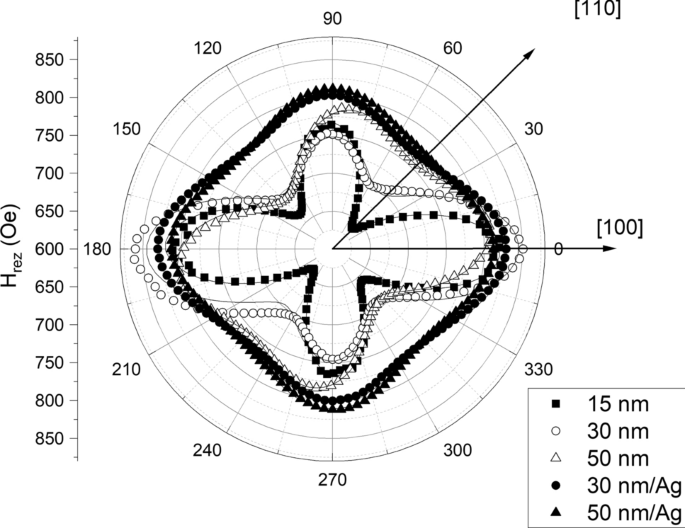
Dipendenza angolare nel piano dei campi di risonanza FMR per i cinque campioni studiati nei nostri esperimenti. Le linee continue rappresentano le curve di adattamento.
La Figura 3 mostra le dipendenze angolari fuori dal piano del campo di risonanza FMR per i cinque campioni studiati nei nostri esperimenti.
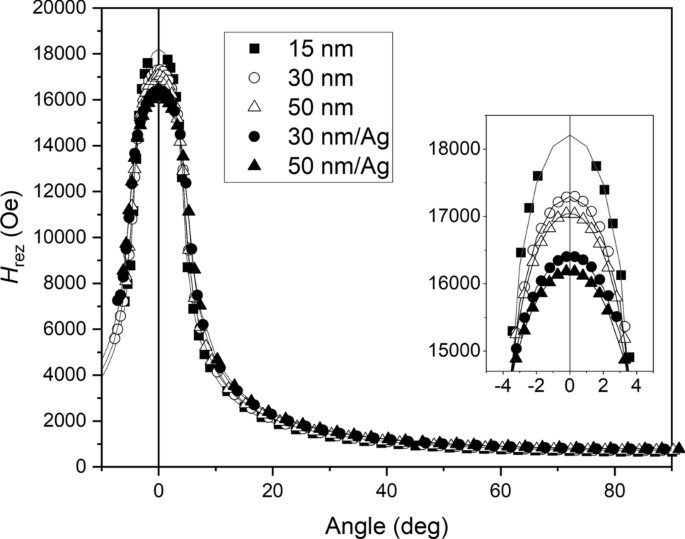
Dipendenza angolare fuori piano del campo di risonanza per i cinque campioni studiati nei nostri esperimenti. Le linee continue rappresentano le curve di adattamento. L’angolo zero corrisponde alla direzione perpendicolare al piano della pellicola. L’inserto mostra un grafico ingrandito con un angolo vicino allo zero.
L’angolo zero nella Figura 3 corrisponde alla direzione del campo magnetico esterno perpendicolare alla pellicola e 90° corrisponde al campo interno al piano della pellicola e parallelo a [110] Asse dello strato magnetico CFMS epitassiale. Si può vedere che aumentando lo spessore dello strato magnetico e aggiungendo lo strato dielettrico Ag si riduce l’entità del campo magnetico risonante verticale, indicando una diminuzione dell’anisotropia magnetica verticale.
Per adattare i dati sperimentali (mostrati nelle Figure 2 e 3), abbiamo utilizzato la formula dell’energia libera per il campione:
$$F = – \mathop \sum \limits_{i = 1}^{3} M_{i} H_{i} + 2\pi M_{s}^{2} \alpha_{3}^{2} – K_{p} \alpha_{3}^{2} + K_{p2} \alpha_{3}^{4} + K_{1} \left( {\alpha_{1}^{2} \alpha_{2} ^{2} + \alpha_{2}^{2} \alpha_{3}^{2} + \alpha_{1}^{2} \alpha_{3}^{2} } \right) – K_{U } \left( {n_{1}^{2} \alpha_{1}^{2} + n_{2}^{2} \alpha_{2}^{2} } \right)$$
(5)
I primi due termini dell’equazione. (5) sono le energie Zeeman e le energie magnetiche statiche. MSè la magnetizzazione di saturazione e H È il campo magnetico esterno. alfaIOIndica la direzione del coseno del vettore di magnetizzazione nel sistema di coordinate associato al campione. La terza coordinata è perpendicolare alla pellicola e la prima è parallela alla pellicola [100] L’asse dello strato epitassiale CFMS. Abbiamo ipotizzato che l’anisotropia fuori dal piano dei cristalli magnetici possa essere descritta dai due termini proporzionali a \({\alpha }_{3}^{2}\) E \({\alpha }_{3}^{4}\)rispettivamente [see the third and fourth term in Eq. (5)]. Il quinto termine dell’equazione. (5) è la variazione del cristallo magnetico cubico con la costante del primo cristallo magnetico cubico \({k}_{1}\). Il sesto termine dell’equazione. (5) descrive la componente nel piano dell’anisotropia uniassiale, il cui asse di facile magnetizzazione è definito dal vettore unitario \({\mathrm{n}}_{\mathrm{i}}\).
I termini di risonanza FMR possono essere calcolati utilizzando una serie di equazioni24:
$$\left( {\frac{\omega }{\gamma }} \right)^{2} = \frac{1}{{M_{s}^{2} \sin^{2} \theta }} \Partire[ {\left( {\frac{{\partial^{2} F}}{{\partial \theta^{2} }}} \right)\left( {\frac{{\partial^{2} F}}{{\partial \varphi^{2} }}} \right) – \left( {\frac{{\partial^{2} F}}{\partial \theta \partial \varphi }} \right)^{2} } \right]$$
(6)
E
$$\frac {\partial F} {{\partial \theta}} = \frac {\partial F} {{\partial \varphi }} = 0 ,$$
(7)
Dove OH è la frequenza angolare, C rapporto giromagnetico, IO E fi sono le coordinate del sistema polare (\(\alpha_{1} = \cos \varphi \sin \theta\), \(\alpha_{2} = \sin \varphi \sin \theta\), \(\alpha_{3} = \cos \theta\)).
La nostra procedura di adattamento ha preso in considerazione le dipendenze del campo risonante angolare nel piano e fuori dal piano e le curve di adattamento sono mostrate come linee continue nelle Figg. 2 e 3. I parametri appropriati sono mostrati nella Tabella 4.
Si può vedere che aumentando lo spessore dello strato CFMS si riduce l’entità della costante di contrasto verticale, KSInoltre, per il campione da 50 nm con uno strato dielettrico aggiuntivo di Ag, KS Cambia segno. Valore negativo per KSCiò significa che è preferita la direzione di magnetizzazione nel piano, mentre un valore positivo favorisce la direzione di magnetizzazione perpendicolare. Tuttavia, la dimensione KS= 1,0×105 erg/cm3 Troppo piccolo per superare l’energia di smagnetizzazione (circa 6,8 x 10,00).6 erg/cm3 Per il campione con lo strato isolante Ag). Per descrivere la dipendenza angolare del campo di risonanza di un campione da 50 nm con lo strato isolante in Ag è sufficiente considerare una sola costante di anisotropia verticale. KS. Nel caso di campioni senza strato di Ag, oltre che di un campione da 30 nm/Ag, per ottenere un migliore adattamento è necessario tenere conto anche della seconda costante di variazione ortogonaleKp2.
Per tutti i campioni esaminati, la prima costante di anisotropia cubica è negativa, il che significa che l’asse di magnetizzazione facile nel piano è parallelo a [110] L’asse dello strato epitassiale CFMS. Tuttavia, l’entità di questa costante diminuisce con l’aumentare dello spessore dello strato CFMS e un’ulteriore diminuzione della sua ampiezza è stata riscontrata dopo l’applicazione dello strato dielettrico Ag. Per descrivere la dipendenza angolare nel piano del campo di risonanza per campioni senza strato di Ag, oltre al campione da 30 nm/Ag, è stato necessario tenere conto anche di una componente aggiuntiva di anisotropia uniassiale,KSh, collocandosi al livello del film. La direzione di questo asse di contrasto non coincide con [100] NO [110] Asse cristallino dello strato CFMS. Tuttavia, per i campioni da 15 nm, 30 nm e 30 nm/Ag, la direzione di questo asse di contrasto è più vicina a [010] Per il campione 50 nm è più vicino [− 110] Asse cristallino dello strato CFMS. Angolo ϕShChe determina la facile deviazione dell’asse della componente nel piano dell’anisotropia uniassiale di [100] L’orientamento dello strato CFMS epitassiale è mostrato nella Tabella 3.

“Studioso di caffè. Appassionato di cibo. Appassionato di birra. Introverso. Praticante di Internet in modo irritante e umile.”






